Pour son anniversaire, Physicus a offert à Mathematicus un joli coffret de montages électroniques ; rien ne pouvait faire plus plaisir à notre ami mathématicien.

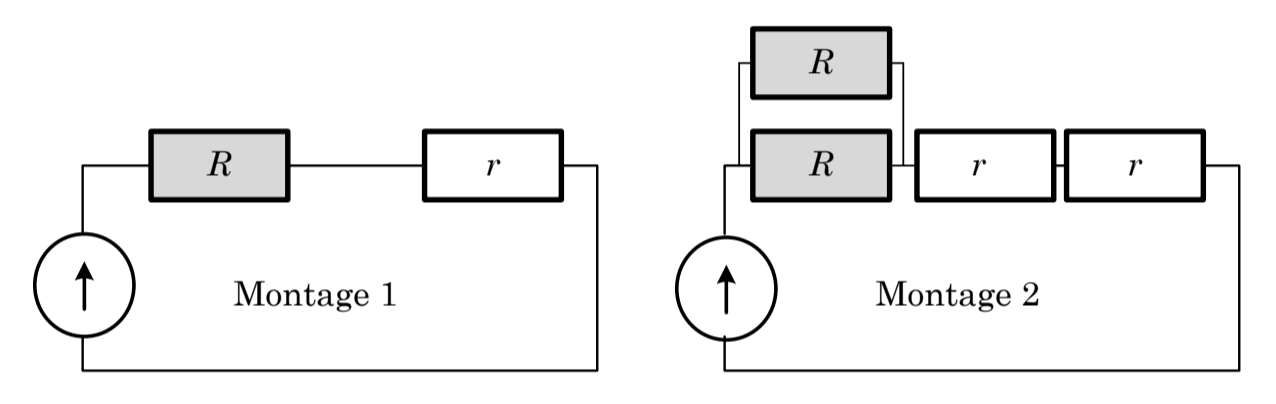
— Regarde mon Montage numéro 1, exulte Mathematicus, fébrile ; je branche en série deux petites ampoules, une grande et une petite, et chacune d’elles s’éclaire.
— Brillant, répond Physicus, imperceptiblement narquois, mais briller, c’est bien ce qu’on demande aux ampoules, me semble-t-il.
— Tu n’y es pas du tout, répond Mathematicus, à qui le trait n’a pas échappé. Mais regarde le Montage numéro deux ! Il est remarquable que lorsque je mets deux grandes ampoules en parallèle et deux petites ampoules en série, alors l’éclairement global produit par les deux grandes ampoules en parallèle du Montage numéro 2 est le même que l’éclairement fourni par la grande ampoule unique, dans le Montage numéro 1.

—Ah ! Voyons cela réplique Physicus, plus intrigué que sceptique.

Il griffonne quelques lignes au dos d’une vague enveloppe et annonce sentencieusement une minute plus tard :

— Le rapport de la résistance de la petite ampoule à celle de la plus grande vaut 0,16 ; voilà pourquoi les deux éclairements sont identiques.
— Montre-moi ça dit Mathematicus, piqué de ne pas avoir résolu spontanément l’énigme … Ah oui, bien sûr, tu considères que les ampoules se comportent comme des résistances pures, ce que tu sais très bien être faux. Jamais, mon cher ami, un Mathématicien n’irait à l’encontre d’un théorème. Mais ce qui m’indigne le plus est que tu donnes une valeur décimale à un nombre qui n’est même pas rationnel.
— Oh ! Si tu veux, mais je doute, mon cher ami, que la précision de tes mesures d’éclairement puisse suivre celle des approximations successives ; allez ! je te le fais à 0,2 et nous sommes quittes.

Mathematicus reste impassible devant ce nouveau trait.

— Je trouve que le rapport des résistances vaut (3√2−1) / 14. Ce n’est pas ce qui apparaît sur ta feuille.
— En effet ; d’ailleurs si je calcule la valeur numérique de ton nombre je trouve… Tiens le bon résultat ! Comment cela se peut-il ?
— Ce qui te surprend, mon cher ami, n’est pour moi qu’un calcul trivial ; disons du niveau de prépa EMC2.
— Tu ne devrais pas te montrer si arrogant, mon cher ami ; autant que je me souvienne, nous étions dans la même prépa et, à leur âge, tu étais bien moins bon qu’eux.

Un silence renfrogné s’installe. Le silence des choses vraies.

Physicus, qui n’a pas l’avantage modeste, renchérit :
— Tes équations ont compris le problème, je n’en doute pas ; mais toi, l’as-tu compris ? Par exemple, moi je peux te dire de tête et sans calcul savant que ton Montage numéro 2 consomme cinq fois plus d’énergie que ton Montage numéro 1. Tu ferais donc bien de tout débrancher avant d’épuiser la batterie.
— Non seulement je débranche, mais encore je range. Je ne saurais rester ton obligé, et serais donc honoré que tu acceptes de ma part cet ouvrage de Abramowitz et Stegun dont tu fis, autant que je me souvienne, un usage copieux pendant ton travail doctoral. Naturellement, je serais heureux d’en parler avec toi, tout comme tu es heureux de parler avec moi de montages.
— Merci souffla Physicus du bout des lèvres.
— Toi, physicien, tu fais des montages et moi, mathématicien, des constructions. C’est ce qui nous rassemble et c’est ce qui nous sépare.

Sur cette flèche du Parthe, Mathematicus s’incline et sort.

1. Quelle est la valeur exacte de r/R, qui garantit l’égalité des puissances consommées globalement dans les parties grisées des deux montages ?
2. Quel est l’argument élémentaire donnant ce facteur cinq ?
3. Est-il si difficile de mesurer des éclairements ?
4. Pourquoi le sarcasme de Physicus sur la précision des mesures de Mathematicus est-il infondé ? En d’autres termes, pourquoi Mathematicus peut-il annoncer que son affirmation peut être rendue vraie au centième ou au millième près ?