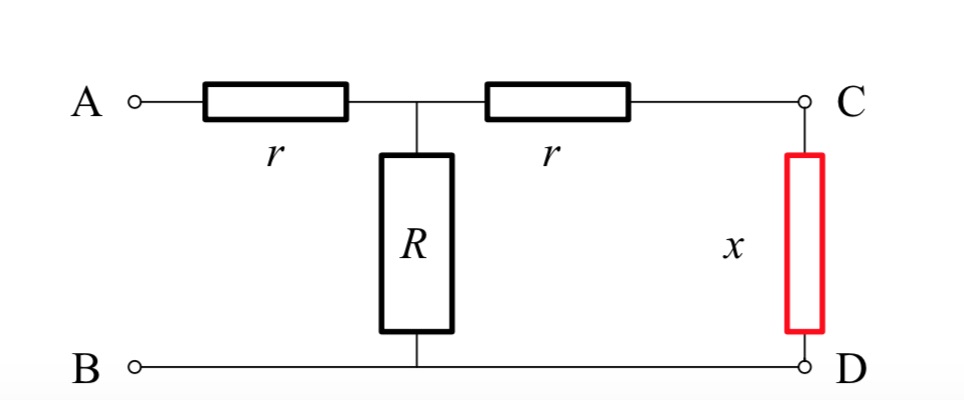
Le jeune Maw Houelle est passionné d’électricité ; sa dernière trouvaille est le circuit de trois résistances ci-contre, qu’il nomme Cellule symétrique en T, pour une raison que lui seul…
Catégorie : Testez-vous
Retrouvez ici des exercices et des énigmes de mathématiques et de physique, élaborés avec soin par l’équipe pédagogique. Pour certains exercices, la solution apparaîtra automatiquement au bout de dix minutes de lecture.

Le Moine et la Voie Unique
Lundi ; 8h37. Le jour et l’heure sont propices. Le Moine, dans la vallée, prend l’unique chemin qui le conduira au sommet de la Montagne Sacrée. Il marche tantôt vite…

Les énigmatiques aventures de Mathematicus et de Physicus – épisode 5
Pour son anniversaire, Physicus a offert à Mathematicus un joli coffret de montages électroniques ; rien ne pouvait faire plus plaisir à notre ami mathématicien. — Regarde mon Montage numéro…

Les énigmatiques aventures de Mathematicus et de Physicus – épisode 4
Pour avoir une idée de la hauteur h où il se trouve, Physicus jette par la fenêtre tout ce qui lui tombe sous la main ; les objets ainsi défenestrés…

Les énigmatiques aventures de Mathematicus et de Physicus – épisode 3
Occupés à composer des énigmes pour EMC2, Mathematicus et Physicus n’ont pas vu le temps passer et, quand ils arrivent à la gare, c’est pour constater que le train vient…

Équation diophantienne
S et N sont deux entiers strictement positifs. Quel est le nombre r(N, P) de solutions de l’équation a1 + a2 + ⋯ + ak + ⋯ + aN =…

Comment séparer N points ?
N points distincts sont répartis au hasard dans un plan ; P est un nombre entier compris entre 1 et N. Construire une droite séparant cet ensemble en deux sous-ensembles,…

Les énigmatiques aventures de Mathematicus et de Physicus – épisode 2
Tiens dit Physicus à Mathematicus, connais-tu la valeur de G la constante de la gravitation ? Les compères ont quelquefois des discussions bizarres. — Et comment que je la connais ! répond…
Les énigmatiques aventures de Mathematicus et de Physicus – épisode 1
Mathematicus fait part de son étonnement à Physicus : « Je suis allé acheter une corde chez Omnibus, tu sais, le type qui tient le Grand Bazar Central, pour entourer une fleur…

Le jeu des tiroirs
Dans 100 tiroirs sont placés aléatoirement 100 papiers numérotés 1 à 100 (permutation de N éléments). Un comparse du joueur a accès au contenu de ces tiroirs et il peut…