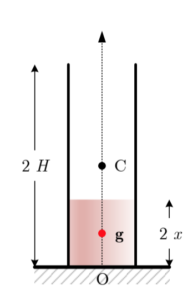
 Un récipient cylindrique est posé sur un plan. Son centre de masse est à mi-hauteur, au point C de l’axe du cylindre. On verse progressivement un liquide homogène dans le cylindre. Le centre de masse de l’ensemble, G, se déplace donc vers le bas. Lorsque le cylindre est complètement rempli, G est de nouveau à mi-hauteur, en C. Il y a donc une situation où G est le plus bas.
Un récipient cylindrique est posé sur un plan. Son centre de masse est à mi-hauteur, au point C de l’axe du cylindre. On verse progressivement un liquide homogène dans le cylindre. Le centre de masse de l’ensemble, G, se déplace donc vers le bas. Lorsque le cylindre est complètement rempli, G est de nouveau à mi-hauteur, en C. Il y a donc une situation où G est le plus bas.
1. Caractériser cette situation, par une propriété remarquable de la position de G.
2. Retrouver ce résultat en mettant le problème en équation, mais sans résoudre l’équation donnant l’altitude de G.
Indications :
1. Comment de déplace le centre de masse d’un système lorsque la répartition de masse, au voisinage d’un point donné de ce système, change ?
2. En un extremum d’une fonction dérivable, la dérivée est nulle.

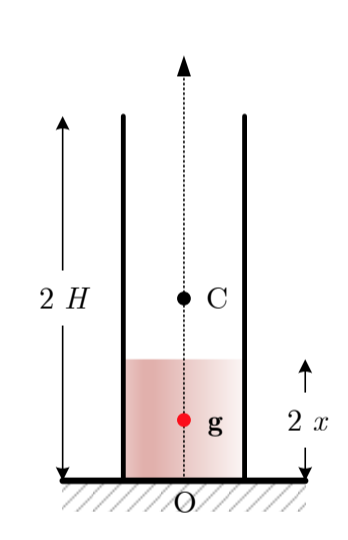
Indication décisive : lorsque l’on ajoute de la masse localisée au centre de masse, la position de ce dernier ne varie pas.