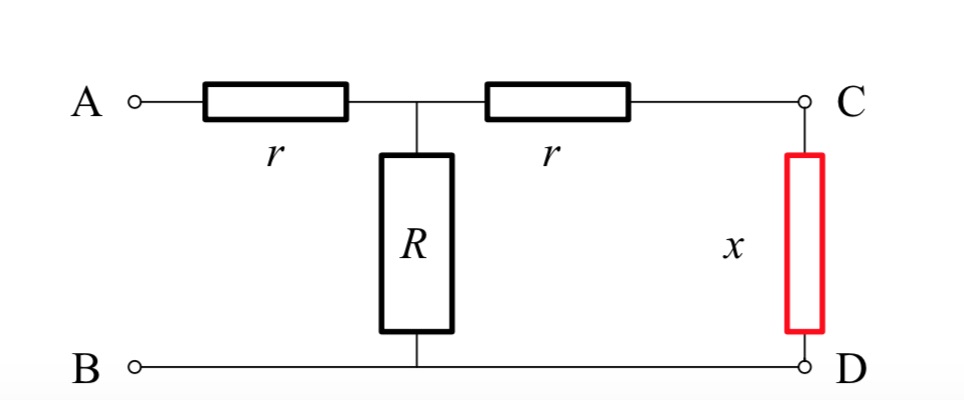
Le jeune Maw Houelle est passionné d’électricité ; sa dernière trouvaille est le circuit de trois résistances ci-contre, qu’il nomme Cellule symétrique en T, pour une raison que lui seul connait.

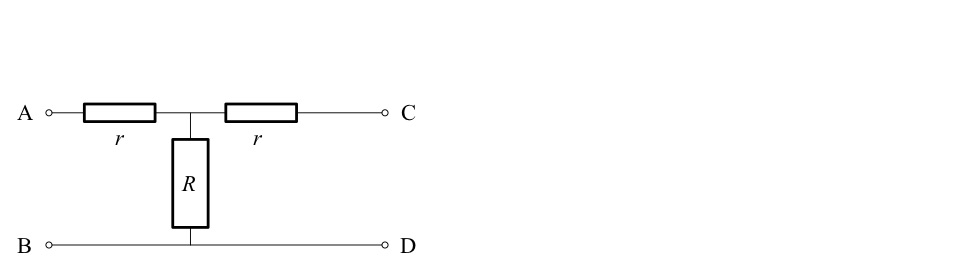
Il en fabrique beaucoup et les assemble en série, c’est-à-dire qu’il joint les points C et D d’une cellule donnée aux points respectivement A et B de la cellule suivante.

Un exemple d’assemblage de trois cellules, fermé sur une résistance de terminaison.

Le 31 décembre 2018, il en met 2018 bout à bout et ferme le circuit par une résistance de terminaison, de valeur x, insérée entre les points C et D de la cellule numéro 2018.

Il mesure alors la résistance entre les points A et B de la cellule numéro 1 et, à sa surprise, il trouve … x.

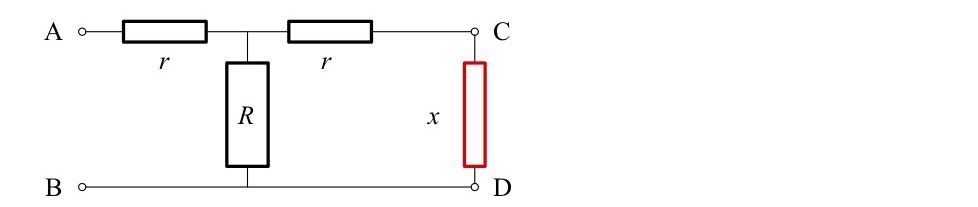
Le lendemain, 01 janvier 2019, il ajoute une cellule à l’ensemble, qui en compte donc maintenant 2019, la dernière cellule étant toujours fermée par la résistance de valeur x. Il retrouve alors que la résistance entre les points A et B de la première cellule garde la même valeur, x.

Emerveillé et intrigué, il s’en ouvre à sa mère, Farah Day qui lui confie : Comme c’est étonnant, j’avais fait la même expérience quand j’avais ton âge, le 31décembre 1993 avec 1993 cellules puis le 01 janvier 1994 avec 1994 cellules. J’avais exactement le même circuit que le tien et, à deux reprises, j’ai aussi trouvé x.

Sur ces entrefaites, arrive le grand-père, Tom Sohn, à qui l’on raconte l’histoire et qui en est éberlué : il y a longtemps, affirme-t-il, je jouais avec les mêmes cellules et avec les mêmes règles : 1958 et 1959 dans mon cas ; la résistance entre les points A et B de la première cellule, avant et après ajout d’une cellule, gardait la même valeur x.

La grand-mère, Pam Dirac, qui n’avait rien perdu de ces effarements, jette alors, négligemment : Ces résultats itératifs n’ont rien de surprenant, le seul hasard heureux est celui qui vous a fait choisir les valeurs de résistances conduisant à de telles propriétés. Considérez, pour le voir, pour 0<a<1, la fonction f :x↦f(x)=(x+a)/(ax+1) ; n’est-il pas immédiat que f(1)=1 ?

Pam a toujours été énigmatique, aux limites de l’insaisissable. Pouvez-vous, sinon la décoder, au moins aider Max, Farah et Tom ?