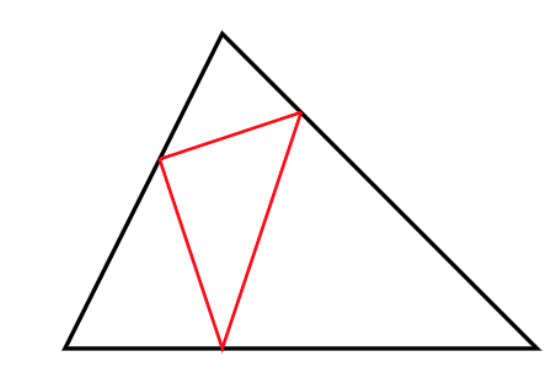
Mathematicus fait part de son étonnement à Physicus : « Je suis allé acheter une corde chez Omnibus, tu sais, le type qui tient le Grand Bazar Central, pour entourer une fleur rare et belle de mon jardin triangulaire ABC. Ce sera comme je te le montre : la corde s’appuiera sur les points a, b et c des côtés de mon jardin.

Figure-toi qu’Omnibus m’a dit qu’il me fournirait gratuitement cette clôture si je pouvais lui garantir, de manière qu’il comprenne l’argument, qu’elle serait la plus courte possible. Alors voilà, je cherche en ce moment la manière la plus simple de caractériser un triangle abc de périmètre minimal, s’appuyant sur les côtés d’un triangle ABC, dont tous les angles
sont aigus. »
— Mais c’est lumineusement simple ! s’écria Physicus.
— Lumineusement ? Et pourquoi ça ?
— Enfin, réfléchis c’est parce que …

Physicus n’avait pas fini sa phrase que Mathematicus courait vers le Grand bazar Central.

Quelle est donc cette solution lumineusement simple ?

Note: il est laissé à la sagacité des lecteurs de placer les points A, B, C, a, b et c.